DataManyo

6.4 선형 판별분석과 선형 커널 서포트 벡터 머신이 어떤 조건에서 같은지 논의하라.

간단하게 설명하면, 선형 서포트 벡터 초평면 w와 LDA 투영 방향 w'가 수직일때 둘은 같다 (그림 참조).

참조:

아래는 iris데이터의 0번째 클래스와 2번째 클래스를 훈련세트로 사용하여 분류한 그림인데, 선형 분리 가능한 데이터에서는 결과값은 크게 다르지 않다는 것을 알 수 있다. 그러나 여기서 말하는 '같은 조건'은 두 경계선이 (결정 함수가) 완전히 일치하는 상황을 뜻한다.

6.3 두 개의 UCI 데이터 세트를 선택하여 선형 커널과 가우스 커널을 사용하여 SVM을 훈련하고 BP 신경망, C4.5 의사결정 트리와 비교하라.

BP 결과는 연습문제 5.6 참조

C4.5 결과는 연습문제 4.6 참조

import pandas as pd
from sklearn import svm
from sklearn import metrics

names = ['sepal length', 'sepal width', 'petal length', 'petal width', 'class']
def loadData(filename):
	dataSet = pd.read_csv(filename, names=names)
	return dataSet

# 데이터세트 분리
def processData(dataSet, n=10):

	values = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
	classifications = []
	gaps = []
	for value in values:
		temp = dataSet.loc[dataSet['class']==value]
		classifications.append(temp)

		gap = temp.shape[0]//n
		gaps.append(gap)

	D = [None for _ in range(n)]
	for a in range(n):
		for gap, classification in zip(gaps, classifications):
			begin = a * gap
			#print(classification[begin:begin+gap])
			if type(D[a]).__name__ == 'NoneType':
				D[a] = classification[begin:begin+gap]
			else:
				D[a] = D[a].append(classification[begin:begin+gap])
			#print(type(D[a]))
			#print(classification[begin:begin+gap])
	return D

def run(data_train, data_test, kernel='rbf'):
	train_data, train_target = data_train[names[:-1]], data_train[names[-1]]
	test_data, test_target = data_test[names[:-1]], data_test[names[-1]]
	
	# SVC() 조정
	'''
	kernel: 디폴트는 ‘rbf’
		선택 가능한 커널 함수：
		‘linear’:선형 커널
		‘poly’：다항식 커널
		‘rbf’：가우스 커널
		‘sigmod’:sigmod커널 함수
		‘precomputed’:미리 계산된 값 사용
	'''
	clf = svm.SVC(kernel=kernel)

	# fit()훈련
	clf = clf.fit(train_data, train_target)

	predict_target = clf.predict(test_data)

	# Accuracy
	acc = metrics.accuracy_score(test_target, predict_target)
	print('Accuracy:', acc)

if __name__ == '__main__':
	filename = '../UCI/iris/iris.data'
	dataSet = loadData(filename)
	D = processData(dataSet, 3)
	data_train, data_test = D[0].append(D[1]), D[2]

	kinds = ['linear', 'rbf']
	for kind in kinds:
		print(kind, end=' ')
		run(data_train, data_test, kind)

6.2 LIBSVM을 사용하고, 수박 데이터 세트 3.0𝛼상에서 선형 커널과 가우스 커널을 사용하여 SVM을 훈련하라. 그리고 각 서포트 벡터의 차이에 대해 비교하라.

*굳이 LIBSVM을 사용하지 않고, sklearn의 svm을 사용해도 무방합니다!

코드는 기본 svm에서 하이퍼파라미터 설정만 바꿔주면 되기 때문에 생략합니다.

일단 다른 하이퍼 파라미터를 사용하면 서포트 벡터가 바뀌게 됩니다. 

수박 데이터세트 3.0a는 선형으로 분리하기 어렵기 때문에 선형 커널을 사용했을 시,

c를 아무리 높여도 오분류 상황이 나옵니다. 

그러나 가우스커널을 사용해 c를 높이면 훈련 데이터에 완전히 핏팅할 수 있습니다. 

c가 비교적 작다면 두 서포트벡터는 비슷하고, c계수가 비교적 크다면(c계수가 클수록 정규화 정도는 낮음)

가우스 커널 서포트벡트의 수는 줄어들지만 선형 커널은 변화가 없을것 입니다.

C=100일 경우,

가우스 커널 서포트 벡터 :  [ 8 9 11 12 13 14 16 2 3 4 5 6 7]

선형 커널 서포트 벡터:  [ 8 9 11 12 13 14 16 2 3 4 5 6 7]

C = 10000일 때,

가우스 커널 서포트 벡터: [11 13 14 1 5 6]

선형 커널 서포트 벡터:  [ 9 11 12 13 14 16 2 3 4 5 6 7]

식과 관련 내용을 복기하면...

점 x의 초평면 상의 투영 점을 x'라고 가정한다면, wTx′+b=0 가 됩니다. 

초평면의 법선벡터는 w이고, 이는 x-x'와 평행입니다. 

그리고,

이기 때문에, 따라서

가 됩니다.

X = array([[1, 0], [0, 1], [0, 0], [1, 1]])

y = array([[1], [1], [0], [0]])

간단한 데이터 세트를 사용해 RBF신경망을 훈련해 봅시다.

여기서는 평균제곱오차를 손실함수로 사용합니다. 출력층은 책과 동일하고, 은닉층의 선형조합을 위해 바이어스항을 추가했습니다.

import numpy as np
import matplotlib.pyplot as plt


def RBF_forward(X_, parameters_):
    m, n = X_.shape
    beta = parameters_['beta']
    W = parameters_['W']
    c = parameters_['c']
    b = parameters_['b']

    t_ = c.shape[0]
    p = np.zeros((m, t_))  # 식5.19
    x_c = np.zeros((m, t_))  # 5.19식에서 x - c_{i} 부분
    for i in range(t_):
        x_c[:, i] = np.linalg.norm(X_ - c[[i],], axis=1) ** 2

        p[:, i] = np.exp(-beta[0, i] * x_c[:, i])

    a = np.dot(p, W.T) + b
    return a, p, x_c


def RBF_backward(a_, y_, x_c, p_, parameters_):
    m, n = a_.shape
    grad = {}
    beta = parameters_['beta']
    W = parameters_['W']

    da = (a_ - y_)      

    dw = np.dot(da.T, p_) / m
    db = np.sum(da, axis=0, keepdims=True) / m
    dp = np.dot(da, W)   

    dbeta = np.sum(dp * p_ * (-x_c), axis=0, keepdims=True) / m

    assert dbeta.shape == beta.shape
    assert dw.shape == W.shape
    grad['dw'] = dw
    grad['dbeta'] = dbeta
    grad['db'] = db

    return grad


def compute_cost(y_hat_, y_):
    m = y_.shape[0]
    loss = np.sum((y_hat_ - y) ** 2) / (2 * m)
    return np.squeeze(loss)


def RBF_model(X_, y_, learning_rate, num_epochs, t):
    '''
    :param X_:
    :param y_:
    :param learning_rate:  
    :param num_epochs:     
    :param t:   
    :return:
    '''
    parameters = {}
    np.random.seed(16)
   

    parameters['beta'] = np.random.randn(1, t)  
    parameters['W'] = np.zeros((1, t))  # 초기화
    parameters['c'] = np.random.rand(t, 2)
    parameters['b'] = np.zeros([1, 1])
    costs = []

    for i in range(num_epochs):
        a, p, x_c = RBF_forward(X_, parameters)
        cost = compute_cost(a, y_)
        costs.append(cost)
        grad = RBF_backward(a, y_, x_c, p, parameters)

        parameters['beta'] -= learning_rate * grad['dbeta']
        parameters['W'] -= learning_rate * grad['dw']
        parameters['b'] -= learning_rate * grad['db']

    return parameters, costs


def predict(X_, parameters_):
    a, p, x_c = RBF_forward(X_, parameters_)

    return a


X = np.array([[1, 0], [0, 1], [0, 0], [1, 1]])
y = np.array([[1], [1], [0], [0]])
#

parameters, costs = RBF_model(X, y, 0.003, 10000, 8)

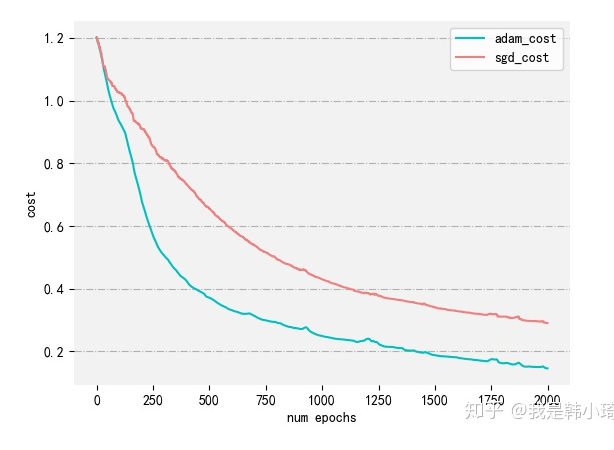
plt.plot(costs)
plt.show()

print(predict(X, parameters))

# 검정
# parameters = {}
# parameters['beta'] = np.random.randn(1, 2)  # 初始化径向基的方差
# parameters['W'] = np.random.randn(1, 2)  # 初始化
# parameters['c'] = np.array([[0.1, 0.1], [0.8, 0.8]])
# parameters['b'] = np.zeros([1, 1])
# a, p, x_c = RBF_forward(X, parameters)
#
# cost = compute_cost(a, y)
# grad = RBF_backward(a, y, x_c, p, parameters)
#
#
# parameters['b'][0, 0] += 1e-6
#
# a1, p1, x_c1 = RBF_forward(X, parameters)
# cost1 = compute_cost(a1, y)
# print(grad['db'])
#
# print((cost1 - cost) / 1e-6)

code출처:https://github.com/han1057578619/MachineLearning_Zhouzhihua_ProblemSets/blob/master/ch5--%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/5.7/RBF.py

동적 조정 방법은 여러가지가 있습니다. RMSProm, Adam, NAdam 등등...

수동으로 하려면 

와 같은 지수 감수 함수를 설정하고 하이퍼파라미터인 r을 조정해주면 됩니다.

구현된 코드는 온라인상에 많으니, 여러가지를 실험해보시길 바랍니다.

여기서는 Adam을 예제로 사용합니다.

https://github.com/han1057578619/MachineLearning_Zhouzhihua_ProblemSets/tree/master/ch5--%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/5.5-5.6

Github링크를 참조해주세요~ (참고용으로만 사용하시고, adam, RMSProp 등에 대한 코드는 많으니 원하는 코드를 검색해 사용하길 추천합니다)

Sklearn의 Iris 데이터로 실험한 결과입니다. 동일한 학습률을 사용할 때 양자(SGD vs ADAM)의 손실함수 변화는 다음과 같습니다:

아담의 수렴속도가 빠르다는 것을 알 수 있습니다.

추가로 하용호 님의 슬라이드 쉐어를 참조하면 도움이 될거에요^^

https://www.slideshare.net/yongho/ss-79607172

사실상 차이는 모든 데이터를 사용해 그래디언트를 계산하하느냐, 데이터 하나만 사용해 그래디언트를 계산하는냐에 있습니다.

코드는 https://github.com/han1057578619/MachineLearning_Zhouzhihua_ProblemSets/tree/master/ch5--%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C/5.5-5.6 여기를 참조 바랍니다.

구현된 코드를 통해 살펴본 결과는 그래프와 같습니다. gd_cost의 수렴과정이 비교적 안정적입니다.

sgd_cost는 항상 최적의 방향으로 수렴하는 것은 아니지만 결국 수렴했고, 200번의 에포크를 돌렸을 때 결과는 크게 다르지 않습니다. 

하지만 확률적 경사하강법(sgd)에서는 매번 반복 할때 마다 하나의 샘플만 사용했기 때문에 계산량에서 큰 차이를 보입니다.

참조:https://zhuanlan.zhihu.com/p/47616848

먼저 학습률이란 무엇인가?

경사하강법에서 파라미터를 업데이트하는 정도를 조절하기 위한 변수이다.

학습률이 너무 크면 오차 함수에서 왔다갔다 하는 폭이 너무 커서 수렴하기 힘들다.

반대로 학습률이 너무 낮으면 수렴이 너무 느려 훈련 효율에 영향을 미친다.

V_ih는 b_h를 계산할 때만 사용하기 때문에,

이고, 여기서 

이기 때문에,

이다.

즉, 식5.13를 얻을 수 있다.

참고답안:

양자모두 연속값을 {0,1}상에 투영하려고 하지만 계단 함수는 매끄럽지 못한 불연속성 성질을 갖고 있기 때문에 시그모이드 함수를 투영 함수로 선택합니다. 다른 점은 신경망에서는 반드시 활성화 함수로 시그모이드를 사용하지 않아도 된다는 점입니다. 비선형성을 가진 미분가능한 함수라면 뭐든 가능합니다.

시그모이드 함수를 활성화 함수로 사용하면 각 뉴런은 로지스틱 회귀와 같아집니다.  단지 로지스틱 회귀에서는 sigmoid(x) > 0.5일때 1을 출력하지만 뉴런은 바로 sigmoid(x)를 출력할 뿐입니다.